La desviación estándar nos indica que tan heterogéneas son las variables en torno a la media. Si su valor es cero entonces son totalmente homogéneos (algo muy raro en la vida real), mientras más se aleje el valor de cero más heterogénea es la muestra.
Se expresa en la misma magnitud de las variables y se suele abreviar como “ds” o “s”.
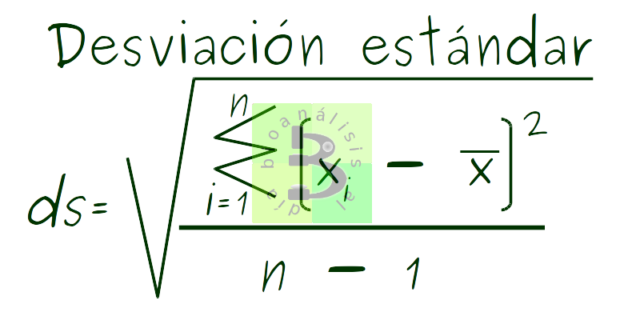
Si bien la media nos brinda una excelente información, esta puede llegar a ser engañosa.
Supongamos que en el laboratorio clínico A, los cinco bioanalistas que trabajan allí ganan 1.000 $ al mes, la media de sus salarios será 1.000$.
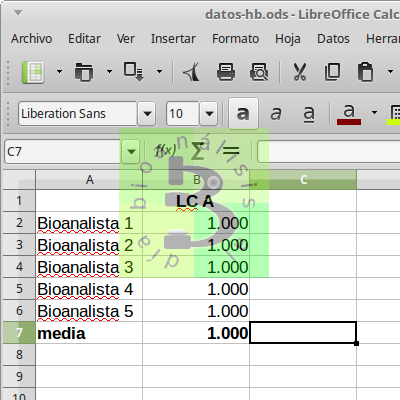
En el laboratorio clínico B, los bioanalistas ganan: 800, 900, 1000, 1100 y 1200 $. La media será de 1.000$.
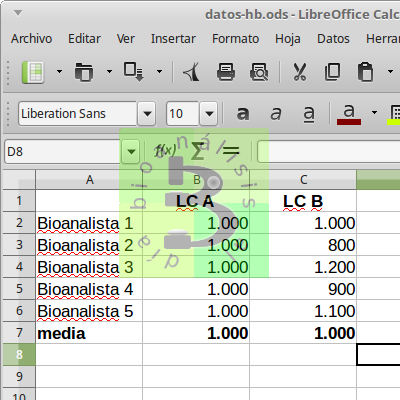
Solamente basados en la media del sueldo (1.000$) en cualquiera de los dos laboratorios el bioanalista recién ingresado gana 1.000$, pero ¿esto es realmente así?
Como conocemos los sueldos individuales sabemos que no, pero es realmente difícil saber todos los sueldos, es más fácil conocer la media y la desviación estándar de una muestra.
La desviación estándar nos indica entonces la variación que existe en torno a la media.
Actividad
Calculemos la desviación estándar (ds) a las dos muestras, mediante la fórmula de la desviación estándar en la hoja de cálculo en español es la de “desvest”
=DESVEST(conjunto de datos)

Para el laboratorio A, la desviación estándar sería 0$, calulemos la ds para el B:
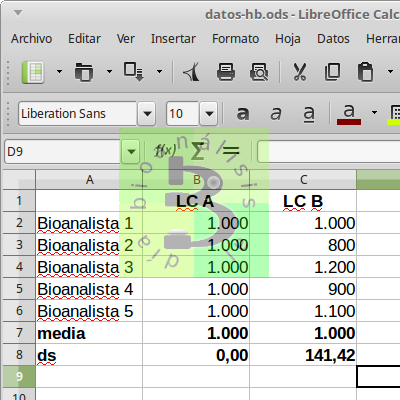
Para el laboratorio A la media es de 1.000 $ y la ds de 0, lo que quiere decir que todos gana lo mismo. En cambio en el laboratorio B, aunque la media es la misma, la ds es de 141.42 $, lo que nos indica que los profesionales del laboratorio clínico ganan sueldos distintos.
Quizás exista una escala o tabla salarial, pero esto no lo podemos concluir, y es un aspecto importante de la estadística, nos dice algo los valores de los estadísticos, pero no nos dice su causa o razón, para ello hace falta tomar en cuenta otros aspectos y realizar lo que se cono como análisis de datos.
Conociendo simplemente la media y la ds de la muestra obtenemos una valiosa información que nos permite conocer a simple vista qué tan similares son la variables y que tan homogéneas son las variables en cada muestra.
Muchas veces los valores de la media y la ds de dos muestras distintas serán muy similares, y hará falta técnicas más finas para conocer si existen diferencias, para ello existe las técnicas estadísticas de contraste de hipótesis para ayudarnos a dilucidar tales situaciones.
Tarea
Calcula la desviación estándar del control de hemoglobina normal, bajo y alto.
Hoy aprendiste
Como obtener la desviación estándar en la hoja de cálculo empleando la función DESVEST. También conociste la utilidad de las llamadas estadísticas de contraste de hipótesis.
Si quieres obtener los datos para hacer el ejercicio, así como realizar el curso completo de estadística básica en hoja de cálculo, registrate aquí