En 1981 se publica en la revista Clinical Chemestry uno de los trabajos de mayor impacto en la calidad en el laboratorio clínico, uno que ha sido bien difundido y popularizado por uno de sus autores, del cual ha tomado su apellido para lograrlo, las multireglas de Westgard.
Se trata de un artículo de lectura obligada para los jefes de calidad o cualquiera que quiera tener un conocimiento profundo sobre el origen y funcionamiento de las multirreglas. Si bien es cierto que ya cumple 40 años, es una publicación totalmente vigente.
J O Westgard, P L Barry, M R Hunt, T Groth, A multi-rule Shewhart chart for quality control in clinical chemistry., Clinical Chemistry, Volume 27, Issue 3, 1 March 1981, Pages 493–501, https://doi.org/10.1093/clinchem/27.3.493
Además de brindarnos los principios básicos del control de calidad interno, que incluye la definición de una regla de control y su utilidad, el fuerte del mismo es la combinación de reglas de control existentes, en un sistema que combina varias reglas, una multirregla.
Shewhart, fue quién recopilo y difundió las ideas del control estadístico de la calidad, para procesos de manufacturación industrial, pero que pueden ser aplicadas a cualquier proceso en el que se debe realizar alguna medición para vigilar la producción. Levey y Jenning tomaron estas ideas y las llevaron al laboratorio clínico, pasando así el gráfico de control de Shewhart a gráfico de Levey Jenning.
Una interpretación equivalente puede ser llevada a cabo con las llamadas reglas de control, las cuales al combinar diferentes condiciones de desviación surgieron una gran cantidad de ellas. Además, los problemas derivados de la confianza que tiene una regla para detectar un aumento del error analítico, generaron diversos debates en cual de ellas era mejor y en que caso de deben aplicar (aún hoy en día existe ese debate, aunque existen mecanismos para aclararlos).
Pero, ¿si se pudiera obtener lo mejor de cada una de ellas en una sola?, de ahí surge la idea de combinarlas en un sistema multirreglas. El artículo en cuestión aborda en profundidad el razonamiento para lograrlo.
Si quieres conocer conocer las reglas básicas de control, tengo preparado esta guía paso a paso para tí.
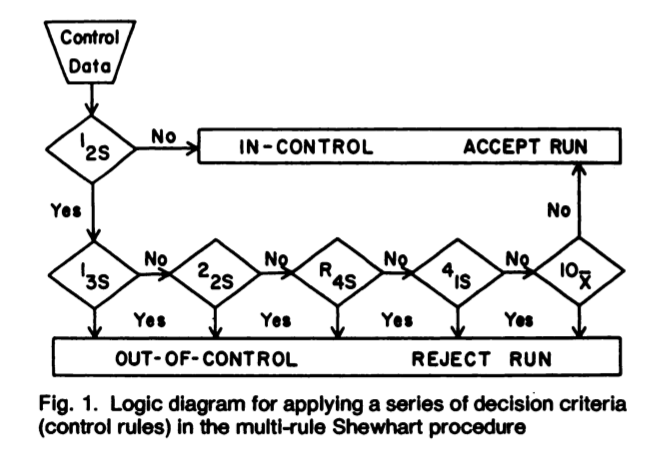
Se explica el funcionamiento de un sistema de control, basado en procesar un material de control por duplicado durante la tanda analítica, razón por la cual el sistema multireglas desarrollado es válido para un material de control procesado dos veces o al emplear dos materiales de control en una tanda analítica. Esta última es la práctica real de los laboratorio clínicos, mientras que la primera es habitual en la industria. De hecho el sistema difundo por Shewhart se basa en procesar el control por duplicado.
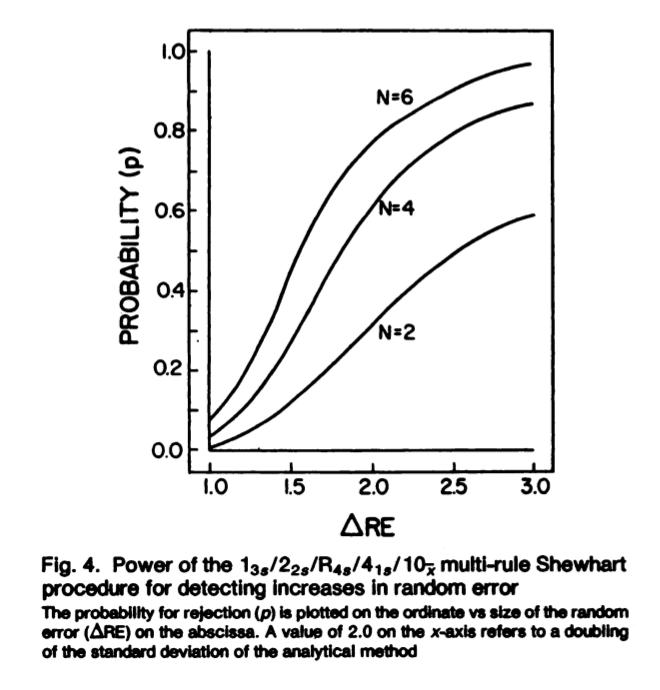
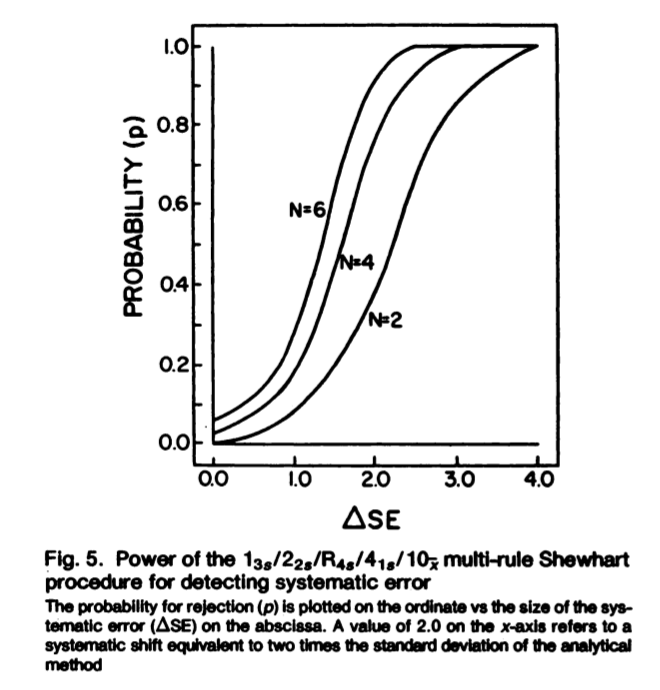
Aparte de la explicación de como se aplica el sistema multireglas propuesto, lo más importante del artículo es la explicación del por que la combinación 1:2s/1:3s/2:2s/R4s/4:1s/10x resulta robusta para detectar aumentos en el error aleatorio y sistemático. Por supuesto que es una explicación basada en estadística, ya que se trata de una aplicación estadística de la calidad.
En todo caso, lo relevante es entender los diversos modelados matemáticos realizados en trabajos previos, y el uso de curvas de poder para detectar los cambios importantes, en forma de probabilidad de detección del error y probabilidad de falso rechazo, medidas relativas a la capacidad de la regla para detectar incrementos del error.
La probabilidad de detección del error debe ser mayor al 90%, que es equivalente a sensibilidad, mientras que la probabilidad de falso rechazo, equivale a un falso positivo, la cual debe ser menor al 5%. De esta manera la regla será eficiente para detectar la mayor parte del incremento en el error analítico, pero con una baja frecuencia de que sea algo debido al azar.
Pues, justamente realizando diferentes combinaciones de reglas, y estudiando su capacidad de detectar incrementos en el error aleatorio o sistemático, llegan a la conclusión que la mejor combinación que respeta esos límites de probabilidad es la multirregla 1:2s/1:3s/2:2s/R4s/4:1s/10x a emplearse en dos materiales de control o un control por duplicado.
La tabla 4 reúne a los diferentes sistemas multirreglas según la cantidad de veces que se procesa el material de control o controles.
Una lectura formidable, que te invito a realizar. Si tienes comentarios, abajo tienes el espacio para plantearlos.
Saludos, y feliz 40 aniversario de las multirreglas de Westgard.
Alfredo Gallardo Acevedo
19 de mayo de 2021
¿Quieres aprender a diseñar el sistema de control interno?
Te enseñaré una metodología robusta para hacerlo >>>>>
Si te ha gustado este artículo, considera suscribirte al boletín de bioanálisis al día
Te activamos y colocamos fibrina a tu conocimiento…